Teaching number skills and concepts with Numicon materials
This paper discusses the use of Numicon number teaching materials with children with Down syndrome. The theory underlying the design of the materials is discussed, the teaching approach and methodology are described and evidence supporting effectiveness is outlined.
Wing, T, and Tacon, R. (2007) Teaching number skills and concepts with Numicon materials. Down Syndrome Research and Practice, 12(1), 22-26. doi:10.3104/practice.2018
The theory
Number ideas are very abstract, and children need to have these presented to them in a wide variety of ways. In the Numicon approach we offer children multi-sensory activities with patterned shapes, rods, number lines, and a broad range of everyday experiences and contexts so that their understanding of number ideas is very richly varied. We do not believe that any single approach or sets of particular apparatus can be adequate in themselves, nor that children will understand numbers just by working with 'figures'.

Figure 1 | Numicon number shapes representing 1-10.
Very importantly in Numicon activities, children can physically combine all patterns, rods, and everyday objects representing numbers with each other in order that their calculating is made 'real'. For example the Numicon patterns themselves physically fit together so that when combining numbers children can physically 'do' the calculations that we want them to 'think'. As they physically combine and compare these patterns they simultaneously 'see' the effects of their actions, and as they speak about what they do and see, their ability to internalise their actions, i.e. 'think with number ideas' gradually becomes secure. In using the Numicon 'feely bag' children learn to relate their physical handling of patterns to their visual impressions, and incorporate both into their growing mental understanding of what number words and figures actually mean; feeling, seeing, thinking, speaking, reading, and writing all come together.

Figure 2 | Part of the Numicon number line.
It is essential that children experience number in a wide range of ways and situations because the wider their experiences the more they will be able to use their understanding in new situations. And connecting their experiences with each other always deepens their understanding greatly. Because children with Down syndrome are relatively strong in their visual thinking, the Numicon approach appeals to their strengths and relies much less on their auditory capacities, with which they generally have more difficulty.
Again essential to Numicon is the belief that because number ideas are so abstract and complex, most children will need to develop them in very small steps. As adults who encountered these ideas long ago, most of us have forgotten just how many times we felt puzzled or simply lost before we gave up and just learned 'how to do sums' without having much of a clue as to what it all meant. The Numicon programme of activities has been developed from innumerable experiences with children in which they have shown us exactly how small many of the steps need to be.
Finally, central to the Numicon approach is the conviction that when children truly feel they understand numbers through physically doing and seeing calculations, their personal self confidence with the ideas will be a key support to them through increasingly difficult later learning. Confidence will encourage perseverance, and perseverance brings success.
The practice
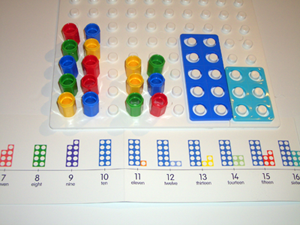
Figure 3 | Numicon pegs grouped to show 16 as 1 ten and 6 units.
It is important that every child meeting Numicon for the first time learns the Foundation activities. As the name suggests, these help children to establish the foundation for success in number. All the materials needed for teaching the Foundation activities are included in the Numicon Foundation Kit, including twelve double-sided, illustrated activity cards which explain the teaching activities. The activities are designed to build up children's skills in small steps. In her recent book [1] , Nye gives helpful suggestions for adapting the activities to the specific needs of children with Down syndrome. Nearly all the activities are designed as games so there is lots of opportunity for turn taking and naturally showing the child what to do when the adult takes a turn; helpfully this means that the activities play to the social strengths of children with Down syndrome. Mathematical language is difficult for all children, so the language that can be developed through each activity is shown clearly on the cards. Of course Numicon is only part of the child's experience with numbers, so on each of the activity cards there are suggestions for making connections with other activities that reinforce the learning and help the child to use and apply the new understanding. Importantly, from the very beginning, children need to be learning and practising their counting alongside all Numicon activities.
The Foundation activities fall into eight broad stages from the earliest familiarisation with Numicon shapes and patterns to practical arithmetic. The first activities are designed to introduce the Numicon shapes and for children to learn to recognise the patterns without using number names or numerals, although they may use number names independently. We suggest that this is encouraged by displaying the Numicon number line which has pictures of Numicon images linked to each number. Several parents have this up permanently where their children can easily reach it. We suggest that children as young as eighteen months can start to become familiar with Numicon, indeed some parents have strung Numicon shapes on ribbons to hang on their children's pushchairs!

Figure 4 | Numicon shapes showing 3 plus 4 equals 7.
The next stage is for children to start to put the shapes in order, again without using number names or numerals. To start with only the first four or five shapes are ordered, gradually building up to ordering all ten. Ordering is such an important activity for mathematical understanding that we suggest also ordering a wide variety of objects so that children can learn the difficult language of size, order and position while playing these activities.
The third stage is to give number names to the Numicon shapes, specifically counting the holes in each shape, filling them with pegs and learning to recognise the numerals. Children then move on to stage four where they order the shapes and the numerals together. This is a huge step for many children and can take some time to master; children are connecting their counting and ordering skills, and as they match the appropriate numeral to each Numicon shape they are learning to order numerals and shapes in relation to each other.
Stage five is really designed to consolidate all the learning achieved up to this point. The activities are designed to help children to confidently recognise Numicon shapes, use number names, recognise numerals, and make connections between their varied counting experiences and the Numicon shapes. Children are also encouraged to consciously visualise the shapes in their minds' eye, preparing for the time when they will cease to rely on actual Numicon shapes because they have a clear mental picture of number that they can use in mental maths.
Children are now ready to begin to understand the structure our 'place value' system so in stage 6 Numicon patterns are used to show how grouping counters into patterns is an efficient way to find out and see 'how many' objects there are in a collection. For instance, 16 objects can be arranged in a Numicon ten-shape pattern and in the Numicon six-shape pattern.
Understanding place value is essential for later work when children learn to add and subtract two and three digit numbers, decimals, money, percentages, multiplication and division. All of which are important for basic numeracy life skills.
Children now have a firm foundation for understanding the sizes and order of numbers, and how numbers relate to one another. They can now begin to relate addition to combining two or more Numicon shapes and learn to use the vocabulary involved in adding.
In this seventh stage children meet their first mental arithmetic strategies: In 'One more' children can see with the Numicon shapes that if you add one to any number it becomes the same as the next number; 'Doubles' are also introduced as special combinations of two numbers.
Subtraction is introduced in the eighth and final stage of the Foundation Kit. It is introduced first as taking away but as you can't actually 'take away' from a piece of Numicon we use the idea of hiding a part of the Numicon shape. The language involved in subtraction is also introduced on these cards. For instance children see that when 1 is taken away from any number the preceding number is always the answer. The tricky 'comparison and difference structure' of subtraction (for example, what's the difference between 8 and 3?) is easily seen by comparing two Numicon shapes.
Children are now ready to move on to Numicon Kit 1 which relates to the English National Curriculum Levels 1 and 2 and the Primary Numeracy Strategy. To check their children's progress and follow through the teaching programme parents can refer to the Numicon Assessment Signposts and Record of Progress, available from Numicon at a cost of £12.50. It is in Numicon Kit 1 that children begin to gain sufficient mathematical understanding to start to understand money and work with simple measures. In Kit 2 children start to work with higher numbers and so are ready to work on measuring in metres and centimetres, litres and millilitres. The Kit 2 work on introducing fractions and multiplication builds the skills children need for learning to tell the time with understanding.
Parents and teachers often ask 'how long will it take to do the Foundation activities?' and of course this will vary hugely from child to child, depending on age and previous experiences as well as aptitude. Older children coming to Numicon for the first time will sometimes move through the stages quite swiftly, some very young children may take three years or more to cover them. What is important to remember is that learning is not a race, every step is significant and is to be celebrated and practised so that children build confidence and positive attitudes. When children enjoy what they are learning they are very likely to be successful. Parents of children with Down syndrome support one another in the use of Numicon through their local associations and there is also a very helpful international discussion group where parents share their successes and questions numiconz@yahoogroups.com. Numicon has five training consultants who specialise in Down syndrome, and full details of the training is available from info@numicon.com.
The evidence
The Numicon approach first began to be developed in 1996 (with UK government funding) by practising teachers in mainstream schools as an approach that would support children of all ages and abilities, and success was quickly shown in dramatically improved SATs scores across the whole ability range [2] .
Devon Education Authority's Primary Maths Team later undertook their own research project into the use of Numicon in mainstream schools during 2003-4, and based upon the success of their findings published a booklet of guidance on the use of Numicon for all Devon primary schools [3] . Apart from this original work in mainstream schools however, several other local education authorities (LEAs) have seen a particular advantage in using Numicon to support children with a range of special educational needs, and have undertaken their own research to test whether the approach really can help children who are finding number work difficult.Between 2001 and 2006, supported and scrutinised by their educational psychology services, Wiltshire [4] , Leeds [5] , and Brighton and Hove [17] LEAs have all independently undertaken teaching programmes based upon the Numicon approach for children who were not succeeding with their school mathematics. Using standard psychological tests to measure results, all studies showed notable improvements in both children's scores and also very importantly in their personal confidence and attitudes to number work. Currently Cambridge and Doncaster LEAs are also trialling the Numicon approach with children with special educational needs, and are reporting very encouraging initial feedback (including again, significantly increased personal confidence in children) informally.
In the Wiltshire project the Numicon approach was used to support specifically children with Down syndrome, and there the reporting educational psychologists found,
"..results to be extremely pleasing in view of the fact that (these) children do not normally make one month's progress per month, yet the average gain exceeds this, and many individuals have improved their skills at a much faster rate than the average." ( REF 4, p.4 )
Down Syndrome Education International has been working with the Numicon approach since 2000 [6-14] . There have also been a number of reports about Numicon in the national journal of the Association of Teachers of Mathematics, Mathematics Teaching [15-17] .
Jo Nye has recently reported [1] on a carefully conducted research project undertaken with 16 children with Down syndrome in Portsmouth, UK. The detailed results from the first year of this project show that all children following the Numicon approach made better progress than other children with Down syndrome not using the system, whilst some children made considerably more progress than their counterparts who were not using the Numicon approach. Other conclusions were that, "[Numicon] enables teaching staff to 'see' what the child is thinking, which is important for identifying both successes and confusions in the child's understanding" ( REF 1, p.3 ), and "Children are motivated to engage with the materials as they are so attractive, and they develop confidence in maths work as they can succeed with the materials" ( REF 1, p.3 ).
Glossary
Numicon
A multi-sensory approach to arithmetic teaching that uses patterns that are structured to encourage the understanding of number and number relationships.
National Curriculum
The statutory teaching curriculum in England for pupils up to the age of 16. It determines the content of what will be taught and sets attainment targets for learning.
Primary National Strategy
A strategy to support teachers and schools to raise standards set out for England by the UK government.
National Curriculum - Key Stages and levels
The English National Curriculum Key Stage 1 is for pupils aged 5-7 years, Key Stage 2 for 7-11 years, Key Stage 3 for 11-14 years and Key Stage 4 for students aged 14-16 years. The programmes of study also map out a scale of attainment within the subject. In most Key Stage 1, 2, and 3 subjects, these attainment targets are split into eight levels. By the end of Key Stage 1 (aged 7), most typically developing children will have reached level 2, and by the end of Key Stage 2 (aged 11), most will be at level 4.
SATs - Standard Attainment Tests
UK National Curriculum teacher assessments and Key Stage tests at the end of Key Stages 1,2 and 3. These give parents and school information about how children are doing.
Relationship to UK Primary National Strategy
Since the Numicon approach was originally developed at the same time as the introduction of the Primary National Numeracy Strategy, both Numicon and the UK government have drawn upon the latest research available on mathematics learning and teaching. Consequently there are key similarities between Numicon and the approaches currently being undertaken in schools (not just in the UK), and this has important implications for parents who wish their children with special educational needs to be included as far as possible in mathematics work with their classmates in schools.
Numicon activities are all cross-referenced to the number objectives of the current Primary National Strategy, and both approaches address the number requirements of the National Curriculum for Mathematics. (Incidentally, in physically manipulating and combining the Numicon patterns children address many of the 'shape and space' objectives as well.) The 'Problem Solving' activities in the Numicon approach closely relate to the categories of problems in the National Strategy, and also to the 'Using and Applying' sections of the National Curriculum.
Very importantly, both the Numicon and Primary Strategy approaches place great emphasis upon the use of visual 'number lines' as central to all children's understanding of number, as well as encouraging as wide as possible a variety of other 'models and images' for numbers. This means that children working with Numicon and its distinctive number lines are developing a mental imagery for numbers that is closely related to that offered in schools for all children. Interestingly also, as many teachers begin to realise that what works with children with special educational needs is also usually good mathematics teaching for all children, a rapidly increasing number of schools are introducing Numicon and making it part of the normal everyday classroom scene for everyone.
A further vital connection between the Numicon and Primary National Strategy approaches is the shared emphasis upon mental arithmetic and how to write down the answers to sums. Because we nowadays ask children to first do sums in their heads (using their mental images), then to say how they did them, and finally to learn how to write down what they have done, children learn first to say, and then to write what are called 'number sentences', e.g.
13 + 5 = 18
This is very different from the Victorian approach most of us learned in schools, called 'tens and units' column recording. 'Tens and units' work was based on a 19th century approach to arithmetic, well before electronic calculators were envisaged, and when every child had to do calculations with paper and pencil from the beginning of their schooling. Modern teaching is based upon children learning mental arithmetic first, and only later learning to do complicated calculations on paper. Consequently, our ways of writing out 'sums' has needed to change to reflect our modern emphasis upon mental arithmetic.
Background of developers and trainers
The developers of the Numicon approach are all graduate (and post-graduate) UK qualified teachers with between them some 85 years experience teaching mathematics to children and students of all abilities, from nursery settings through to university level. Until very recently, all were full time teachers working in schools and university implementing the National Numeracy Strategy with children of all abilities - which of course is the challenging context in which the Numicon approach was first developed.
Five of the team of Numicon consultants who undertake training in the use of the approach are experienced in teaching children with Down syndrome and three of them are themselves parents of children who have Down syndrome. All the Numicon consultants are, like the authors, formally qualified teachers with a great deal of successful experience teaching mathematics in schools, with one exception - Dr Joanna Nye (formerly at Down Syndrome Education International) is a practising research psychologist at the University of Bristol, UK.
Box 1 | Materials required and costs
Individual use
To begin with an individual user would need to buy the Numicon Single User Foundation Kit @ £86 + VAT. As the child begins to make progress with this first stage, it would be helpful to buy also a set of Number Rods @ £30 + VAT.
The Numicon Kit 1 Plus Pack then supports the middle phase of the Numicon programme, and this currently costs £76 + VAT.
The current final phase of the Numicon programme is supported with the Numicon Kit 2 Plus Pack @ £64 + VAT.
Thus the current whole Numicon programme, taking the learner from the first introduction to basic number ideas through addition, subtraction, multiplication, division, and problem solving, would cost £256 + VAT to support an individual learner.
Class use
The cost to a school for the equivalent whole class kits would be:
Foundation Class Kit @ £120 + VAT
Kit 1 Class @ £160 + VAT
Kit 2 Class @ £180 + VAT
A set of Number Rods £30 + VAT.
References
- Nye J. Teaching number skills to children with Down syndrome using the Numicon Foundation Kit. Portsmouth: Down Syndrome Education International, 2006. ISBN: 978-1-903806-92-0.
- https://www.numicon.com/Assets/Downloadablefile/Learning%20about%20numbers%20with%20patterns.pdf
- Devon Primary Maths Team. An Image of Number: the use of Numicon in mainstream classrooms. Exeter, UK: Devon County Council, 2006.
- Ewan C, Mair C. Wiltshire Pilot Project - Numicon (March-July 2001). Down Syndrome News and Update. 2002; 2(1): 12-14. doi:10.3104/practice/159.
- Leeds Primary National Strategy Team. Multi-sensory approach to the teaching and learning of mathematics - Pilot Project 2005. Leeds, UK: Education Leeds, 2005.
- Buckley SJ, Bird G. Number skills for individuals with Down syndrome - An overview. Portsmouth, UK : Down Syndrome Education International, 2001.
- Bird G. Number skills for infants with Down syndrome (0-5 years). Portsmouth: Down Syndrome Education International, 2001.
- Bird G, Buckley S. Number skills for children with Down syndrome (5-11 years). Portsmouth: Down Syndrome Education International, 2001.
- Buckley SJ, Horner V, Wing T, Bird G. The Numicon approach. Down's Syndrome Association Journal. 2001;98:18-22.
- Nye J, Buckley SJ, Bird G. Evaluating the Numicon system as a tool for teaching number skills to children with Down syndrome. Down Syndrome News and Update. 2005;5(1):2-13.
- Uttley W. Introducing numbers and Numicon to young children who find it difficult to sit and concentrate. Down Syndrome News and Update. 2003;3(1):18-19.
- Uttley W. An update on Sam and the progress he has made in numeracy using Numicon. Down Syndrome News and Update. 2004;4(1):15-16.
- Saunders E. Number fun? You can count on it! Down Syndrome News and Update. 2004;4(1):11-14.
- Lander A. Feely Bags. Down Syndrome News and Update. 2006;6(1):14-15.
- Horner V. Numicon, numeracy and a special need. Mathematics Teaching. 2002,179, p.28-31.
- Wing T. Serendipity and a special need. Mathematics Teaching. 2001;174:27-30.
- Saunders S. Joining Luke's Wires. Mathematics Teaching. 2005;191:31-33.
Received: 2 February 2007; Accepted 14 February 2007; Published online: 30 July 2007.

