Numerical ability, general ability and language in children with Down syndrome
The aims of this study were to investigate the relationship between numerical and general ability and the contribution that receptive language makes to numerical ability in children with Down syndrome. Sixteen children with Down syndrome were tested on the following measures: two nonstandardised tests of numerical ability, two standardised numerical tests, two measures of receptive language and an IQ scale. Only one of the sixteen children attained a score on the IQ measure so the relationship between general and numerical ability in this population could not be assessed. All four numerical measures significantly correlated (positively) with each other, and receptive grammar (but not vocabulary) was found to significantly correlate (positively) to numerical skills. Details of the children's performance on the two main numerical measures under investigation are presented.
Nye, J, Clibbens, J, and Bird, G. (1995) Numerical ability, general ability and language in children with Down syndrome. Down Syndrome Research and Practice, 3(3), 92-102. doi:10.3104/reports.55
Introduction
The study reported here investigated the numerical ability of children with Down syndrome, and the relationship between numerical ability and general ability in these children. The contribution of receptive language to numerical skills was also examined.
Numerical Processes in the Typical Population
The study of numeracy covers a wide range of abilities making use of a variety of experimental methods and populations (see Dehaene, 1992, for review). Areas of research include investigation into the adult representations of numerosity, formal calculation processes and the role of notation within these two areas. The developmental processes that lead to a fully operational numerical system have also been extensively researched. In these fields there are many unresolved issues.
One of the main controversies in this area is how much numerical processes are influenced by general cognition, or whether they are discrete modules (e.g. Shipley and Shepperson, 1990; Gallistel and Gelman, 1990). A wider debate also exists about the nature of general cognitive ability and its relationship to specific abilities (see Anderson, 1992). Gelman and Gallistel (1978) assert that the development of children's counting is guided by domain-specific principles, whereas Shipley and Shepperson (1990) argue that the general ability to process discrete physical objects enables them to identify what to count (preceding the acquisition of counting principles) and also operates in some aspects of language acquisition. This work has been enhanced by studies of patients with brain-lesions (e.g. McCloskey, 1992), particularly supporting conceptions of numerosity as a set of modular processes rather than as a unified concept. Various models have been developed to describe how these different abilities interact (e.g. Dehaene, 1992).
Calculation is intuitively seen to be linked with language processes, because it makes use of the ability to mentally manipulate sequences of symbols. Consequently numeracy has sometimes been thought to be part of the language faculty with no need to be seen as separate (e.g. Hurford, 1987). It would appear however that there are some numerical abilities that do not use mental representations based on language or numerical notation (Dehaene, 1992). This approach should not be taken to mean that the role of linguistic processes has been totally disregarded: as Dehaene's model describes, numeracy involves a complex set of abilities, some of which are based on the mental manipulation of symbols (e.g. mental arithmetic) and some of which are not (e.g. representations of numerosity).
This debate forms part of a more general controversy over whether language is a distinct system or the product of general learning or cognitive processes. There is strong evidence that language is modular and that it can be further divided into sub-modules (Clibbens, 1993).
One of the essential elements of numeracy is the ability to quantify sets of data. It has been suggested that three main processes are used in quantification which are counting, subitization and estimation (Klahr and Wallace, 1973). Counting is the most well established concept, being best defined by the five principles of Gelman and Gallistel (1978). The existence of these principles is well supported and a great amount of research has focused on their development. Despite this a controversy remains over whether a skeletal set of these principles is innate (Gelman and Gallistel, 1978), guiding the acquisition of counting behaviours, or whether the principles are progressively extracted after repeated practice with rote learning procedures (e.g. Fuson, 1988; Siegler and Shipley, 1987).
Subitization is the process whereby very small sets (below 3 or 4) are quantified immediately and estimation is used to quantify a large number of items. The exact processes involved have not been precisely defined (Dehaene, 1992) and it is disputed whether they actually exist separately from counting as defined by Gallistel and Gelman (1992).
A manifestation of the general ability view of numerical skills is the theory proposed by Piaget (1952). Piaget argued that children will develop mathematical concepts in their own time. Central to these concepts is number conservation, the understanding of which is thought to precede all arithmetical operations. This theory has been influential in the structuring of educational provision but has been criticised by researchers such as Donaldson (1978) and Gelman and Gallistel (1978). The main criticism has been that children are able to demonstrate understanding of conservation at younger ages than Piaget claimed, if appropriate methodologies are used.
Alternative methodologies (e.g. the 'Magic' paradigm used by Gelman and Gallistel, 1978) provide indirect evidence that three- or four-year-old children can also understand addition and subtraction. For Piaget understanding of these transformations does not occur until six or seven years. Support for Gelman's claims comes from Hughes (1981) who provided more direct evidence of such understanding, as long as the situation presented to the children was based in some sort of context.
The Cognitive Development of Children with Down Syndrome
Down syndrome is a chromosomal disorder, which causes a specific pattern of physical and developmental characteristics. It is now generally accepted that all children born with Down syndrome will have learning disabilities, but the severity of the disability will vary between individuals (Carr, 1985).
One of the main debates surrounding cognitive development in Down syndrome is whether it progresses through the same stages as typical development but at a slower pace or whether it is qualitatively different (Lewis, 1987). It may be that some abilities develop in a different way to that of typically developing children, while others emerge at a slower rate. Support for this view comes from a review of the literature on language skills in Down syndrome (Rondal, 1987). A further possibility is that milestones are reached in the same order as typically developing children, but that the underlying developmental processes are different (e.g. the 'developmental difference' theory proposed by Morss, 1985). Each of these positions has implications for educational provision and for theoretical issues in the wider study of child development.
Numerical Ability in Children with Down Syndrome
Down syndrome has been the focus of much research, partly because the syndrome is identifiable from birth and also because Down syndrome is the largest sub-division of the learning disabilities (Lewis, 1987). One area of study that has been largely neglected in this population is numerical ability (Bird and Buckley, 1994). The following is a review of the only studies found which investigate the numerical abilities of children with Down syndrome. There is a basic understanding of the sorts of numerical abilities that the children can be expected to achieve, with present educational programmes. There are also some beginnings into investigating the numerical processes that the children are using but it is clear that there is a need for further investigation with this group.
Cornwell (1974) concluded that children with Down syndrome learn to count using rote procedures and do not develop understanding of arithmetical concepts. This finding was used to illustrate a general difficulty in concept formation and abstraction. Gelman and Cohen (1988) made use of the conclusion that children with Down syndrome only count using rote learning to investigate the controversy about whether typically developing children are guided by counting principles (Gelman and Gallistel, 1978) or gradually extract the principles after using rote counting procedures (e.g. Fuson, 1988; Siegler and Shipley, 1987). They found that generally the children with Down syndrome were not as able as mental age matched pre-schoolers in solving a novel counting problem. Due to the general difference between the two populations the results supported the argument that typically developing children make use of counting principles. However two of the children with Down syndrome were found by Gelman and Cohen to be 'excellent counters' who were able to make use of principled counting, but most of the children did not display such ability. They stress that we cannot conclude from these results that children with Down syndrome cannot take advantage of counting principles and that with appropriate intervention this may be possible.
Caycho, Gunn and Siegal (1991) matched children with Down syndrome with typically developing children of a similar 'developmental level' (using the Peabody Picture Vocabulary Test - Revised), rather than using mental age for matching. There was no significant difference between the two groups in performance on tasks testing the counting principles. Therefore, it was concluded that children with Down syndrome can make use of counting principles and their counting competence is related to receptive language not to the syndrome itself. Again it was stressed that the ability to take advantage of the counting principles may be a function of the type of educational programme the children are engaged in, and that it must not be assumed that all children will develop such understanding, just that they are capable of doing so.
Surveys of the children's abilities have also been carried out (e.g. Buckley and Sacks, 1987; Carr, 1988; Irwin, 1989). These have described the levels of attainment that the particular cohort of children reached at the time but do not give detailed insight into the processes that the children are using or techniques that are useful for developing numerical skills.
Intervention studies that have been tried with children with Down syndrome have also been reported. Irwin (1991) found that children with Down syndrome who could 'count-all' were able to master 'counting-on' (counting-on from the largest addend) for addition, using a structured teaching technique. The children were able to generalise the skill to materials not used for teaching. The Macquarie programme (Thorley and Woods, 1979; Pieterse and Treloar, 1981) was a teaching programme based on the work of Gelman and Gallistel (1978) which reported a variety of results with a small group of children. Two children mastered all the objectives of the programme, with one developing further skills. The remaining children mastered between 1 and 16 objectives, out of 38.
One issue that has been studied is how useful estimates of general ability and labels such as Down syndrome or learning disability are in predicting numerical ability. Two studies have provided contradictory evidence about this (Baroody, 1986; Sloper, Cunningham, Turner and Knussen, 1990).
Sloper et al (1990) found a significant correlation between mental age and numerical ability (r = 0.73). They investigated the academic achievement, including numerical ability, of 117 children with Down syndrome (aged 6 to 14 years). Academic attainment was measured by questionnaires (filled in by the children's teachers) which assessed a range of numerical competencies from "Discriminates between largest and smallest groups of objects" to "Does simple division work" (see Table 2 for complete set of items). The children displayed a wide range of abilities. Overall educational attainment was found to correlate with mental age and type of school attended, with mainstream schools being connected with higher educational attainments. This was supported by Casey, Jones, Kugler and Watkins (1988) who found similar benefits for children with Down syndrome attending mainstream schools, including in numerical ability.
Baroody (1986) tested 100 'mentally handicapped' children (though not specifically Down syndrome) using a series of games investigating numerical skills which children are expected to have when entering school in the US. These include tests of Gelman and Gallistel's five counting principles. Baroody found wide individual differences, with some children with lower IQs (33-49) in the younger age group (6 to 10 years) performing at a higher level than some of the children with higher IQs (51-80) in the older age group (11 to 14 years). Baroody concluded that labels such as IQ are not useful in predicting levels of numerical ability. The conclusions that these two studies make regarding the use of knowledge about general abilities for prediction of numerical skills are starkly different, and the reasons for this difference must be looked at more carefully.
One of the most prominent differences between the two studies is the population examined. Although this may seem an obvious reason why the two studies have different results, the predictions from either could be used to inform intervention and theory about children with Down syndrome. A further (possible) difference between the studies is the general ability measure used. Baroody (1986) made use of IQ scores but the exact tests used to obtain these are not described. Indeed it is not clear whether the children were even tested using the same measure. To obtain mental age scores, Sloper et al. (1990) used the McCarthy Scales of Children's Abilities (McCarthy, 1972) and for children who did not attain a score on the McCarthy, the Bayley Scale of Infant Development (Bayley, 1969). In addition the two studies cover a very different range of numerical ability. The Baroody (1986) test only covers the skills that a typically developing child would have on entering school in the US (aged six years) and the Sloper et al (1990) checklist ranges from early skills up to arithmetic.
The current study was designed to test the hypothesis that the scores attained by children with Down syndrome on the test used by Baroody (1986) and the scale used by Sloper et al (1990) will positively correlate with each other, both being claimed to be measures of numerical ability. Two standardised tests of numerical ability from the British Ability Scales (Elliott, 1987) and the Kaufman Assessment Battery for Children (Kaufman and Kaufman, 1983) were also used to test the validity of the two unstandardised tests. It was predicted that if the Baroody and Sloper scales do indeed measure numerical ability they should both positively correlate with existing standardised scales.
In addition an IQ measure (the British Ability Scales) was employed to test the hypothesis that there would be a positive correlation between IQ and numerical ability, as tested by the four different measures. From this the previous conclusions that Sloper et al (1990) and Baroody (1986) reached were investigated further using the same benchmark of general ability. Conclusions about the relationship between numerical ability and 'general ability' may not necessarily be taken further as debate surrounds what general cognitive ability consists of and whether it is measured by IQ (Anderson, 1992).
To investigate the contributions of language to numerical ability, because of the conclusions drawn by Caycho, Gunn and Siegal (1991), the children were also tested on the British Picture Vocabulary Test (Dunn, Dunn, Whetton and Pintilie, 1982; the British standardised version of the Peabody Picture Vocabulary Test). To extend the investigation of the contribution of language skills further the Test for Reception of Grammar (Bishop, 1983) was also used. Chronological age, schooling history and gender were also collected for analysis. (Females with Down syndrome have been found to be more advanced in general development and have higher IQ scores than males (Carr, 1985) so it may be a relevant variable for numerical skills.) The hypothesis that receptive language, chronological age, schooling history and gender all significantly correlate with numerical ability was tested (using the Sloper et al (1990) checklist and Baroody (1986) tasks for the measures of numerical ability).
Methodology
Design
The study was of a within subjects/correlational design, with all participants being tested on the same battery of standardised and unstandardised tests. The order of presentation of the battery of tests varied between subjects but this was not manipulated systematically.
Subjects
The 16 children who participated in the study all had Down syndrome. Eight were female, eight male. They were aged between 7;0 and 12;6 (mean age: 8;9) at the time of testing. All attended mainstream primary schools.
Procedure
The children involved in the current study were already being studied as part of a research project conducted by staff at the Sarah Duffen Centre, University of Portsmouth. The current research fell under the informed consent that the parents and teachers had already given. Supplementary information about the project was provided during individual visits. In addition it was made clear that the child concerned did not have to take part in any of the tests that the parents or teachers were not happy with (maintaining the ethical standards for informed consent) and that all results would be confidential.
Each child was tested in a quiet area within their school, at the Sarah Duffen Centre (a research centre with facilities for assessing children) or at the child's home. The first author administered all the numerical tests. The remaining tests were randomly administered either by this same experimenter or one other experimenter as part of the wider study. The battery of tests was administered to each child over several sessions, across one or more days, varying with individual children's levels of fatigue and attention. If any child displayed discomfort or unwillingness to perform any of the tasks, testing on an individual task was discontinued.
Measures
Baroody Numerical Test
A series of tests based on those used by Baroody (1986) to identify basic counting skills was used with the children. (From here on this group of tests will be referred to as the 'Baroody Numerical Test'.) Rather than using the criterion levels for each item that Baroody used to compare groups, a continuous scale of scores was implemented to aid correlational analysis. Therefore, each child could score between 0 and 136 points on this test. Where necessary, test item materials were constructed from copyable teaching workbooks. The set of tests were:
-
Oral Counting - the child is asked to count up to 40, both with and without materials.
-
Counting by Tens - counting 10 counters marked as 10p pieces.
-
Enumeration and Production of Objects - in the context of a shopping game the child is asked to count sets of objects and count out specified numbers of objects.
-
Cardinality Rule - a set of objects is counted in front of the child, the display is covered and the child is asked how many objects have been hidden.
-
Order-Irrelevance Principle - counting sets of blocks in various directions.
-
Finger Representations to 10 - ability to hold up a specified number of fingers quickly.
-
Equivalence - this test involves the child identifying a picture from a set of three, which matches a stimulus picture.
Teacher Questionnaire
Class teachers and/or classroom assistants were asked to complete a rating scale of the child's numerical ability, as constructed by Sloper et al (1990) which was based on a checklist devised by Lorenz (1985). This checklist comprises 22 levels starting from "discriminates between largest and smallest group of objects" to "does simple division sums" followed by "can do more advanced number work. Please specify . . ." (see Table 2 for complete set of items). Each item on the checklist is scored as "Can't do" (score = 1); "Can do with help" (score = 2); or "Can do" (score = 3), with a possible range of scores between 22 and 66. The checklist was presented to the teaching staff with a front cover, which included instructions for completion of the checklist, spaces for recording education details about the child and who the form was completed by.
Subject Data
The chronological age of the child and amount of time they had spent in mainstream schooling was collected from the class-teachers or classroom assistants in conjunction with the 'Teacher Questionnaire'.
Standardised Tests
The following standardised tests were carried out with the children:
-
British Ability Scales (Elliott, 1987) - various sub-scales. These included the numerical ability scale and the scales required to calculate the short-form IQ. For children aged 5;0 to 7;11 years these are: recall of digits, similarities, matrices and naming vocabulary. For children aged 8;0 to 17;5 years these are: recall of digits, similarities, matrices and speed of information processing;
-
Kaufman Assessment Battery for Children (Kaufman and Kaufman, 1983) arithmetic scale;
-
British Picture Vocabulary Scales (Dunn, Dunn, Whelton & Pentillie, 1982) which measures receptive vocabulary;
-
Test for the Reception of Grammar or TROG (Bishop, 1983).
| Possible Score | Current study | Sloper et al study | |
|---|---|---|---|
| Mean | - | 40.12 | 31.04 |
| Standard dev. | - | 6.40 | 8.93 |
| Minimum | 22.00 | 28.00 | 22.00 |
| Maximum | 66.00 | 49.00 | 64.00 |
Results
Educational Details
Complete details of all the children's schooling histories were not readily available but the information that was obtained from class teachers and special needs assistants indicated that the children had highly individual patterns of education. Because of the complex nature of this variable it was not used in the statistical analyses, but a summary is given here to describe the population studied.
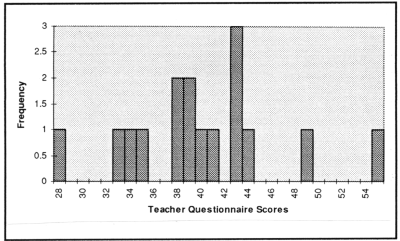
Figure 1. Distribution of scores on Teacher Questionnaire.
Twelve of the children had attended mainstream schools for the whole of their education so far, while two had transferred from special schools at some point. Two of the children had attended mainstream school part-time for a period, with one of these also attending a special school part-time. Further information about where the second child spent the remainder of the week, whether at home or at another school, was not available. The length of time each child had spent in a particular type of education varied from one to five years. One child had been kept back to repeat a year. Details of pre-school groups or interventions were not readily available.
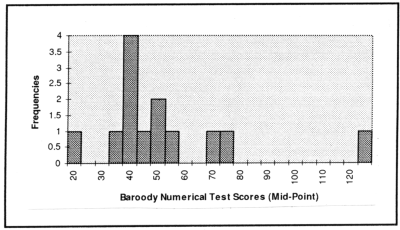
Figure 2. Distribution of scores on Baroody Numerical Test.
Teacher Questionnaire
The distribution of the scores on the Teacher Questionnaire is presented in Figure 1. Table 1 shows the mean, standard deviation, minimum and maximum scores obtained. The table also shows the results found by Sloper, Cunningham, Turner and Knussen (1990) using the same measure in their study of 117 children with Down syndrome. A higher mean score and a lower standard deviation can be observed in the current study. (These differences have not been tested for significance.) Differences between the two samples of children with Down syndrome should be noted. The sample of 16 children in the current study had a mean age of 8;9 years (range 7;0 to 12;6) and the sample of 117 children in Sloper et al. (1990) had a mean age of 9;2 years (range 6;0 to 14;0). All the children in the current study attended mainstream schools. In the Sloper et al. (1990) study the children attended a variety of schools, including mainstream and those for children with severe and moderate learning disabilities.

Table 2. Results form the Teacher Questionnaire (Sloper et al., 1990)
To look at abilities of individual children the full results of the Teacher Questionnaire are presented in Table 2, with the children in order of chronological age. Wide variation can be seen in the pattern of abilities, with no simple pattern of progression with age across the group. For the majority of the children skills up to Item 8 (writes symbols, 0 to 9) have been acquired or can be performed with help. From Item 9 (writes symbols, 10 to 20) the majority of the children either cannot perform the skill or can only do so with help. This is even more pronounced after Item 13 (subtracts from written number up to 9, without materials).
This is a very general description of the performance of this group, and it is clear from Table 2 that there are wide individual differences in performance. The main exceptions to this description are children 1, 15 and 16; one of the youngest and the two oldest children. Child 1 is able to perform the first six skills on the questionnaire with help from an adult. The two oldest children can do, or can do with help, items across the whole range of the questionnaire, being unable to do only three or four of the items.
| Possible Score | Current study | |
|---|---|---|
| Mean | - | 52.87 |
| Standard dev. | - | 24.35 |
| Minimum | 0.00 | 20.00 |
| Maximum | 136.00 | 126.00 |
Discussion
A significant positive correlation was found between the Teacher Questionnaire and the Baroody Numerical Test. This indicates that they measure overlapping sets of numerical skills. They both significantly correlate (positively) with the two standardised measures of numerical ability (the British Ability Scales and the Kaufman) and this supports the construct validity of the nonstandardised tests as measures of numerical ability. This conclusion should be made with caution as the tests have not been tested for reliability (a prerequisite for validity) and have only been tested on a limited sample in this study.
As the children (apart from one) did not obtain IQ scores on the British Ability Scales, the hypothesis that there would be a positive correlation between the numerical test scores and the IQ scores could not be tested. It would therefore be useful to replicate this study with a general ability test that was more appropriate for the population studied, in an attempt to resolve the conflicting conclusions of Sloper et al (1990) and Baroody (1984). Exactly what general ability consists of and how it can be measured is a controversial issue (Anderson, 1992). Research by Shipley and Shepperson (1990) suggests that the general ability to process discrete objects guides children's counting behaviours and they draw attention to literature that indicates that this ability also aids vocabulary acquisition.
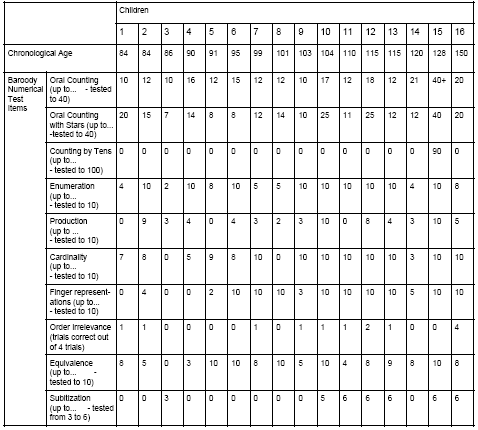
Table 4. Results form the Teacher Questionnaire (Sloper et al., 1990)
To investigate the relationships between numerical skills and other variables further, the hypothesis that receptive vocabulary, receptive grammar, chronological age, school history and gender would all significantly correlate with numerical ability was tested. The details of the children's educational background were complex and consequently were not used for analysis. All of the children were attending mainstream school at the time of testing, but their school histories leading up to this point were highly individual. The finding that gender does not correlate with the numerical ability scores is inconsistent with previous evidence (Carr, 1985).
Caycho, Gunn and Siegal (1991) studying children with and without Down syndrome, found that use of the counting principles was related to receptive vocabulary rather than mental age. In the current study small positive correlations exist between the four numerical scales and the BPVS, but these are not significant.
The numerical skills that Caycho, Gunn and Siegal (1991) were investigating were the use of Gelman and Gallistel 's (1978) counting principles, whereas the numerical scales in the current study cover a wider range of numerical skills. The counting principles are only explicitly tested by a sub-set of items in the Baroody Numerical Test which has the smallest correlation coefficient with the vocabulary scale out of the four numerical tests. The current study, not having looked specifically at the counting principles, cannot provide evidence to either support or refute the claims of Caycho et al (1991).
In contrast to the relationships between receptive vocabulary and the other variables, receptive grammar (as measured by the Test for Reception of Grammar; Bishop, 1983) was found to correlate with all numerical measures, as well as chronological age and receptive vocabulary. That receptive vocabulary and grammar differ in their correlation with numerical skills, may be due to different numerical skills being related to different aspects of language, as suggested by Dehaene (1992). From the current study numerical ability has a greater relationship with receptive grammar than vocabulary knowledge in this group of children.
The nature of the relationships found between numerical ability and aspects of language is relevant to the discussion about Dehaene 's (1992) model of numerical processes, in which he supports the study of different populations for the development of a comprehensive theory. Dehaene provides convincing evidence that numerical processes need to be seen as separate from the language faculty, which is the position supported by Hurford (1987). Dehaene describes how some numerical processes (those using verbal numerical notation) are based on linguistic functioning but that some are completely independent (e.g. representations of numerosity). The current research supports the ideas implicit in Dehaene's work that different numerical competencies are related to different sub-modules of language (e.g. lexical and syntactic systems).
Baroody's description of the skills of typically developing children entering school in the US at age 6 does not transfer to the British education system, either for age or for policy of meeting children's special needs at school. It would be informative to conduct a study of typically developing children at infant schools in the UK to make more meaningful comparisons about the skills achieved by the children with Down syndrome in the current study.
The group of children studied here do not show a steady progression of numerical skills with chronological age (from the Sloper et al. (1990) questionnaire). It is likely that this is due to individual differences. A major factor in this is likely to be the numeracy training that the children receive, which up to now has been given little attention (Bird and Buckley, 1994). Improvements in the teaching of reading to children with Down syndrome have improved performance to levels that were once thought unattainable (Bird and Buckley, 1994) suggesting that it is worth investigating intervention techniques which could enhance numerical skills. Therefore further research needs to carried out into teaching numerical ability, both in schools and in pre-school programmes. In addition, research into the underlying numerical processes and acquisition of these in this population is also required.
Using the label of Down syndrome in isolation has been thought to have little use in determining educational provision including for numeracy and arithmetic skills (Bird and Buckley, 1994). Preconceived ideas about limits on performance are thought to be highly restrictive, causing self-fulfilling prophecies. Baroody's research into children with learning disabilities supports this. As the current study could not test the hypothesis that general ability is related to numerical ability, nothing further can be added to the debate about the usefulness of general ability for prediction. Although measures of receptive language could be used to give some indication of the level that numerical skills teaching should be aimed at, it would be far more appropriate to use measures of numerical skills with the individual child for planning educational intervention.
Caution should be taken in interpreting the results found here because of the small sample studied. With this population it is often necessary to study small populations and for this reason it may be more appropriate for future studies to focus on more detailed analysis of patterns of performance, including errors. For example, Baroody (1986) was able to study the errors that the children made on the numerical tasks. Gelman and Cohen (1988) made detailed analysis of the patterns of responses that the children gave to novel counting problems. One of the problems with the current study was the difficulty of recording all the children's responses accurately, while administering all the test items. A solution to this would be to use video recording equipment, enabling detailed analysis of error patterns. Such analysis would also complement research using statistical analysis with larger samples such as the one carried out by Sloper et al (1990) who studied 117 children with Down syndrome.
Conclusion
In children with Down syndrome all four measures of numerical ability are useful for assessing numerical ability. The four tests have different characteristics which could be taken advantage of in different situations. The two standardised tests (from the British Ability Scales and the Kaufman Assessment Battery for Children) can be used by psychologists where appropriate and for calculation of standardised scores if they are required. For professionals, such as teachers, who do not have training/access to use standardised tests both the Sloper Questionnaire and the Baroody Numerical Test can be used to assess a range of numerical skills. The Teacher Questionnaire is particularly useful for accessing the knowledge that teachers and assistants have about a child that may not perform to their best ability in a simple test situation. It also enables the collection of a large amount of data, as in the Sloper et al (1990) study. The Baroody Numerical Test is designed to make the test situation child-centred, with most of the tasks being built into a game. It is a useful test for a detailed assessment of counting skills. In addition many of the tasks can be adapted to become training tasks (Baroody, 1992).
No conclusions could be drawn from the present study about the relationship between numerical ability and general ability. Receptive grammar was found to correlate significantly with numerical ability.
More work is required to determine how these skills and underlying processes are developing and how remediation programmes can be best designed to aid the development of numerical ability in children with Down syndrome.
Acknowledgements
This research was conducted as part of a B.Sc. Psychology (Hons.) degree at the University of Plymouth.
Many thanks to all the children who took part in this study and to the head teachers, class teachers and parents who allowed me the pleasure of working with their children.
I am deeply indebted to the staff at the Sarah Duffen Centre, particularly Sue Buckley, Gillian Bird and Angela Byrne for their support while setting up the project and collecting my data.
References
- Anderson, M. (1992). Intelligence and Development: A Cognitive Theory. Oxford: Blackwell.
- Baroody, A.J. (1986). Counting ability of moderately and mildly handicapped children. Education and Training of the Mentally Retarded, 21, 289-300.
- Baroody, A.J. (1992). Remedying common counting difficulties. In J. Bideaud, C. Meljac and J.-P. Fischer (eds.), Pathways to Number: Children's Developing Numerical Abilities. Hillsdale, NJ: Lawrence Erlbaum Associates.
- Bayley, N. (1969). Manual for the Bayley Scales of Infant Development. New York: The Psychological Corporation.
- Bird, G. and Buckley, S. (1994). Meeting the Educational Needs of Children with Down Syndrome. Portsmouth: University of Portsmouth. Available Online: https://www.down-syndrome.net./library/books/meeting-ed-needs/
- Bishop, D.V.M. (1983). Test for the Reception of Grammar (TROG). University of Newcastle-upon-Tyne.
- Buckley, S. and Sacks, B. (1987). The Adolescent with Down Syndrome. Portsmouth: Portsmouth Polytechnic.
- Carr, J. (1985). The development of intelligence. In D. Lane and B. Stratford (eds.), Current Approaches to Down Syndrome. London: Holt, Rinehart and Winston.
- Carr, J. (1988). Six weeks to twenty-one years old: A longitudinal study of children with Down syndrome and their families. Journal of Child Psychology and Psychiatry, 29 (4), 407-431.
- Casey, W., Jones, D., Kugler, B. and Watkins, B. (1988). Integration of Down syndrome children in the primary school: A longitudinal study of cognitive development and academic attainments. British Journal of Educational Psychology, 58, 279-286.
- Caycho, L., Gunn, P. and Siegal, M. (1991). Counting by children with Down syndrome. American Journal on Mental Retardation, 95 (5), 575-583.
- Clibbens, J. (1993). From theory to practice in child language development. Down Syndrome: Research and Practice, 1 (3), 101-106. [Read Online ]
- Cornwell, A.C. (1974). Development of language, abstraction, and numerical concept formation in Down syndrome children. American Journal of Mental Deficiency, 79 (2), 179-190.
- Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44, 1-42.
- Donaldson, M. (1978). Children's Minds. London: Fontana.
- Dunn, L.M., Dunn, L.M., Whetton, C. and Pintilie, D. (1982). The British Picture Vocabulary Scale. Windsor: NFER-Nelson.
- Elliott, C.D. (1987). British Ability Scales. Windsor: NFER-Nelson.
- Fuson, K.C. (1988). Children's Counting and Concepts of Number. New York: Springer-Verlag.
- Gallistel, C.R. and Gelman, R. (1990). The what and how of counting. Cognition, 34, 197-199.
- Gallistel, C.R. and Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition, 44, 43-74.
- Gelman, R. and Cohen, M. (1988). Qualitative differences in the way Down syndrome and normal children solve a novel counting problem. In L.Nadel (ed.), The Psychobiology of Down Syndrome. Cambridge, MA: MIT Press.
- Gelman, R. and Gallistel, C.R. (1978). The Child's Understanding of Number. Cambridge, MA: Harvard University Press.
- Hughes, M. (1981). Can pre-school children add and subtract? Educational Psychology, 1, 207-219.
- Hurford, J.R. (1987). Language and Number. Oxford: Basil Blackwell.
- Irwin, K.C. (1989). The school achievement of children with Down syndrome. New Zealand Medical Journal, 102, 11-13.
- Irwin, K.C. (1991). Teaching children with Down syndrome to add by counting-on. Education and Treatment of Children, 14 (2), 128-141.
- Kaufman, A.S. and Kaufman, N.L. (1983). Kaufman Assessment Battery for Children. Minnesota: American Guidance Service.
- Klahr, D. and Wallace, J.G. (1973). The role of quantification operators in the development of conservation. Cognitive Psychology, 4, 301-327.
- Lewis, V. (1987). Development and Handicap. Oxford: Blackwell.
- McCarthy, D. (1972). Manual for the McCarthy Scales of Children's Abilities. New York: The Psychological Corporation.
- McCloskey, M. (1992). Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia. Cognition, 44, 107-157.
- Morss, J.R. (1985). Early Cognitive Development: Difference or Delay? In D. Lane and B. Stratford (eds.), Current Approaches to Down Syndrome. London: Holt, Rinehart and Winston.
- Piaget, J. (1952). The Child's Conception of Number. London: Routledge & Kegan Paul.
- Pieterse, M. and Treloar, R. (1981). The Macquarie Program for Developmentally Delayed Children: Progress Report 1981. Macquarie University, Australia.
- Rondal, J.A. (1987). Language development and mental retardation. In W. Yule and M. Rutter (eds.), Language Development and Disorders. Oxford: Blackwell.
- Shipley, E.F. and Shepperdson, B. (1990). Countable entities: Developmental changes. Cognition, 34, 109-136.
- Siegler, R. and Shipley, C. (1987). The role of learning in children's strategy choices. In L. S Liben (ed.), Development and Learning: Conflict or Congruence? Hillsdale, NJ: Lawrence Erlbaum Associates.
- Sloper, P., Cunningham, C., Turner, S. and Knussen, C. (1990). Factors relating to the academic attainments of children with Down syndrome. British Journal of Educational Psychology, 60, 284-298.
- Thorley, B.S. and Woods, V.M. (1979). Early number experiences for pre-school Down syndrome children. Australian Journal of Early Childhood, 4, 15-20.

